推荐系统

Apriori关联分析算法

• 无监督
• 挖掘关联
• 数据集很大时，运行效率低（故用FP-Growth优化）

Apriori（支持度） 组合购买数不大于 支持度 就被淘汰

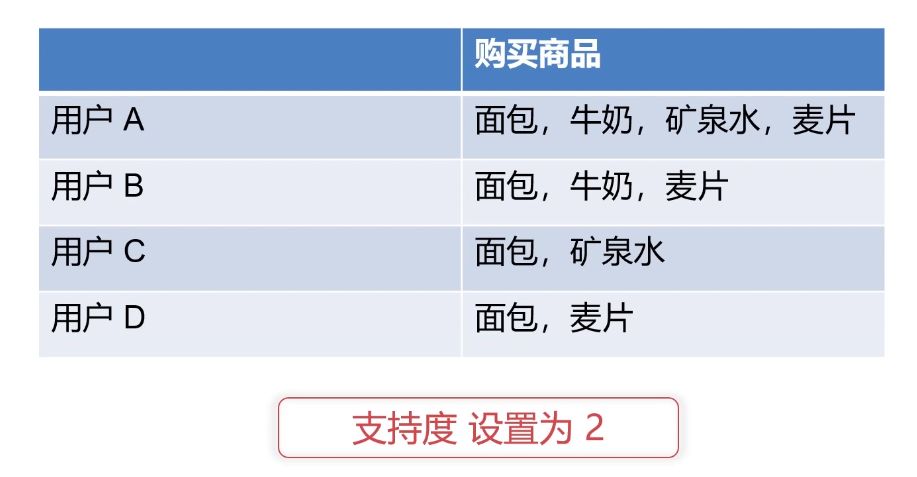
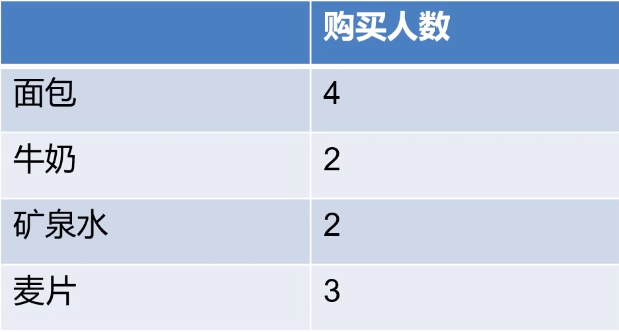
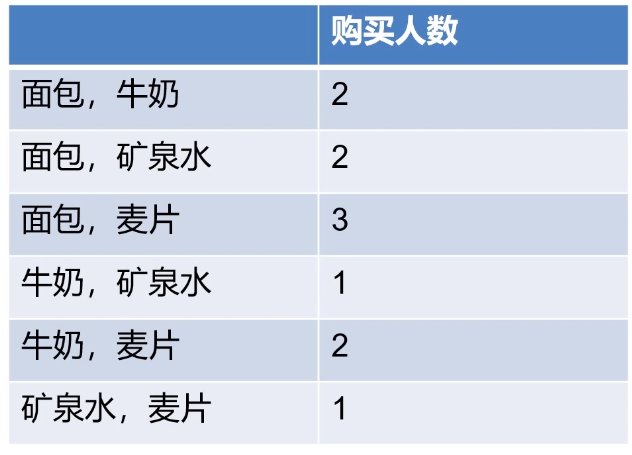
下图购买人数全部大于支持度*2，故都不淘汰

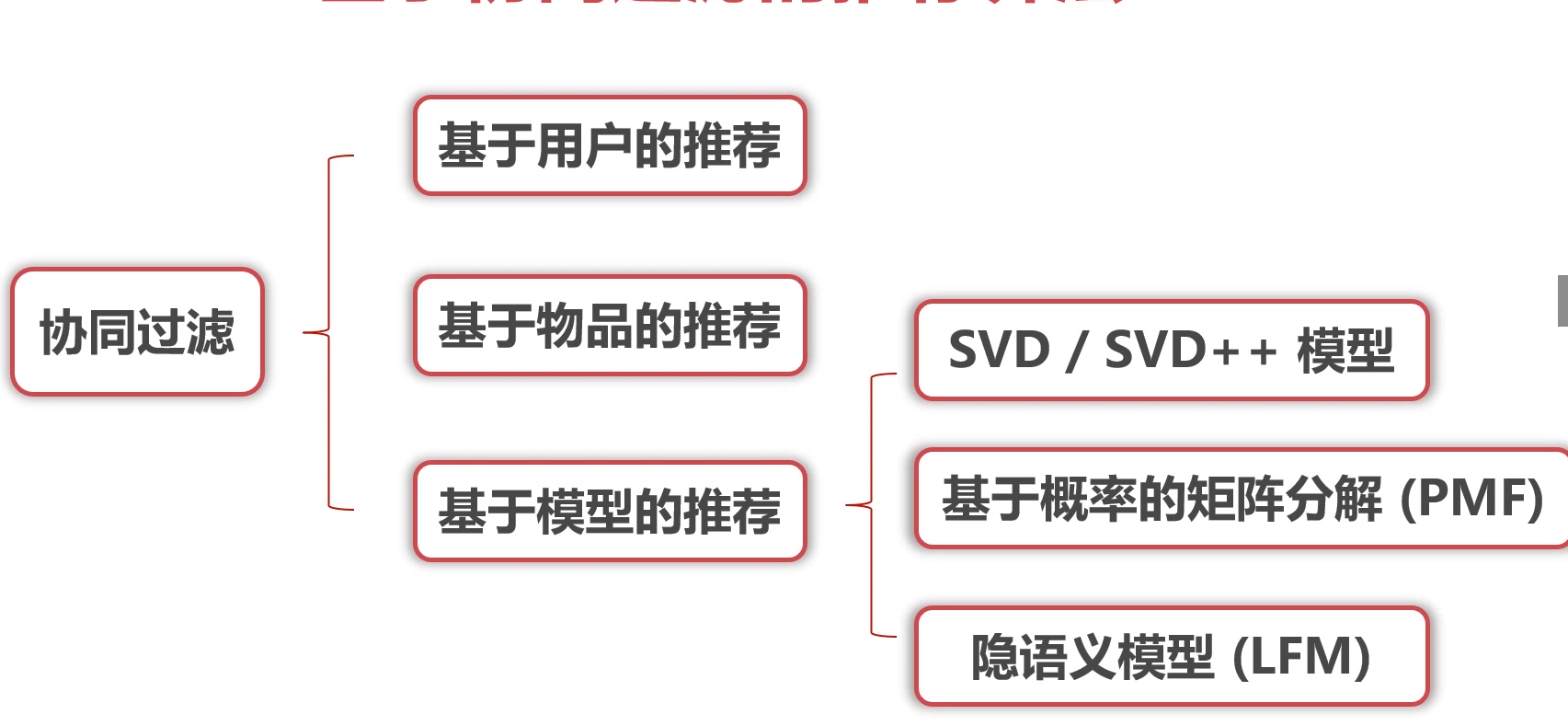
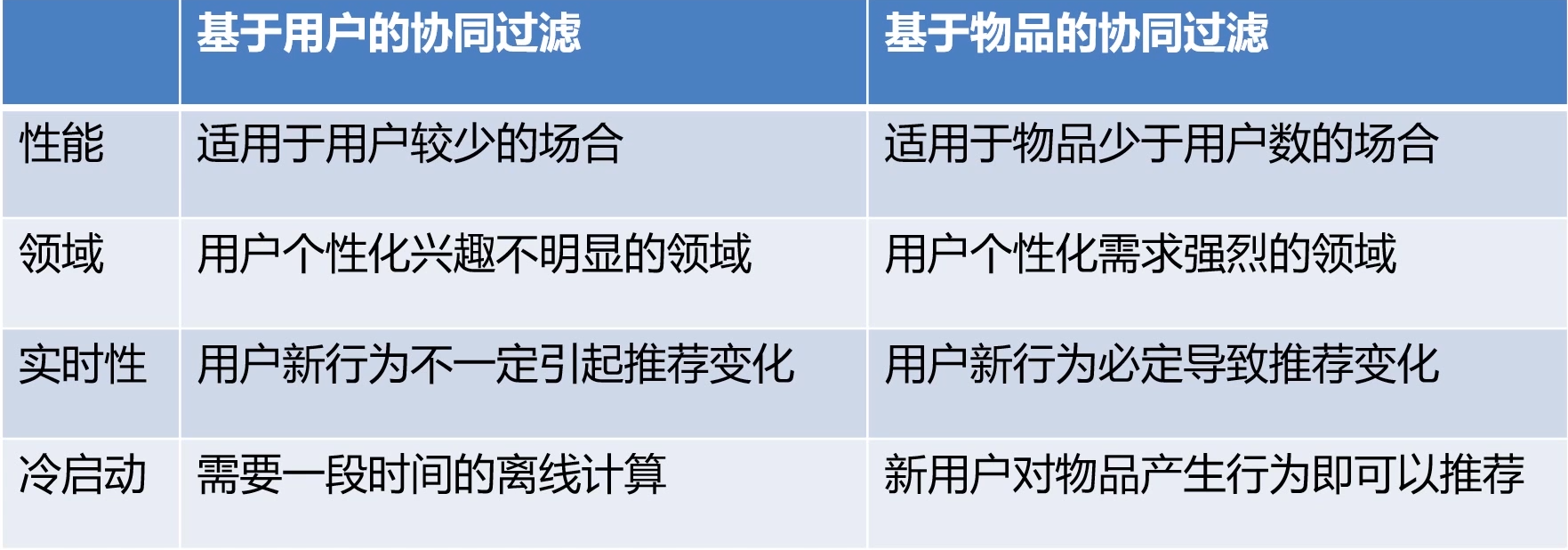
• 缺点
  • 数据稀疏性和冷启动问题
• 优点
  • 挖掘用户的潜在兴趣
  • 仅仅需要评分矩阵来训练矩阵分解模型

推荐系统常见的问题

• 冷启动（数据问题）

  • 用户冷启动→新用户
  • 物品冷启动→新物品
  • 系统冷启动→新系统
  • 根据注册信息 进行分类（邮箱 性别 手机号码）
  • 推荐热门的排行榜
  • 基于深度学习的语义理解模型
  • 引导用户把属性表达出来
  • 利用用户在社交媒体的信息

• 数据稀疏（算法优化的问题）

• 不断变化的用户喜好

• 不可预知的事项（千人千面）

物品冷启动：

离线实验：数据集上完成试验

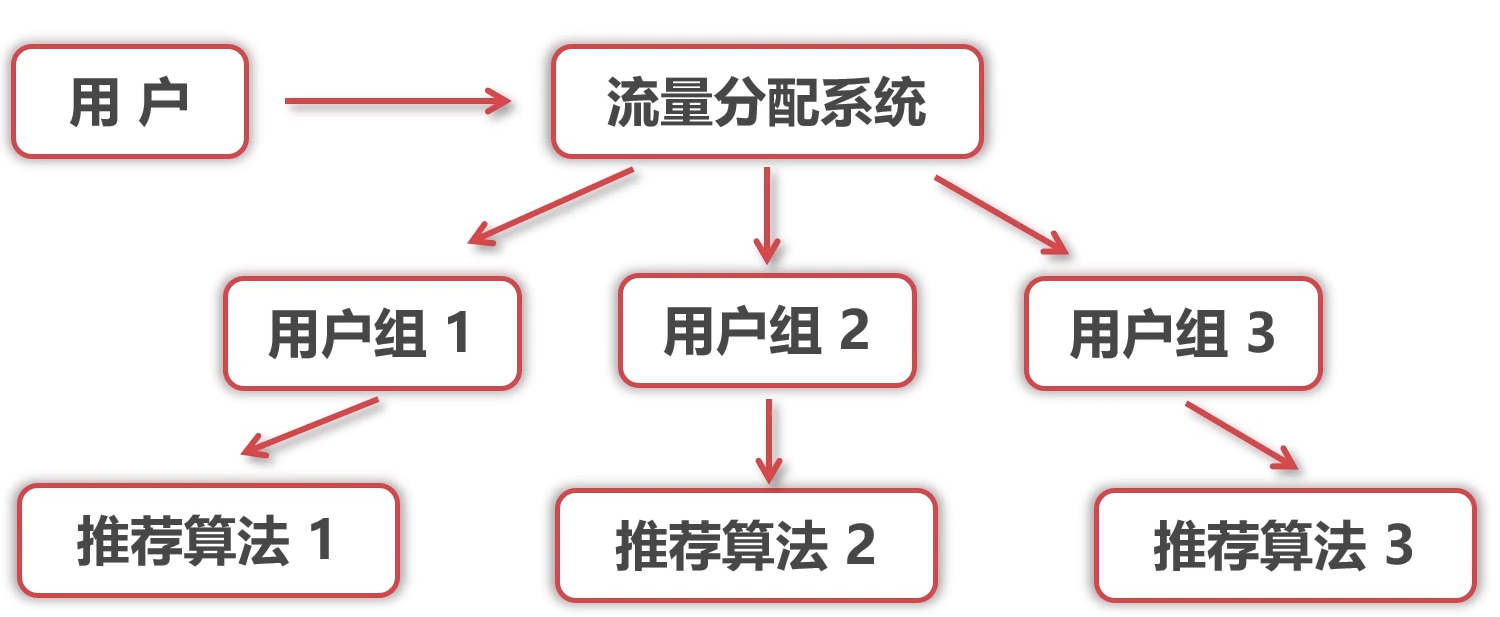
A/B Test在线实验 分几组 每组进入不同模型

用户调研和反馈

A/B Test在线实验

• A/B Test 在线实验是以正交分桶为基础（随机将用户划分几组）
• 根据分桶执行不同的算法得出差异化的指标
• 取其中较优的算法

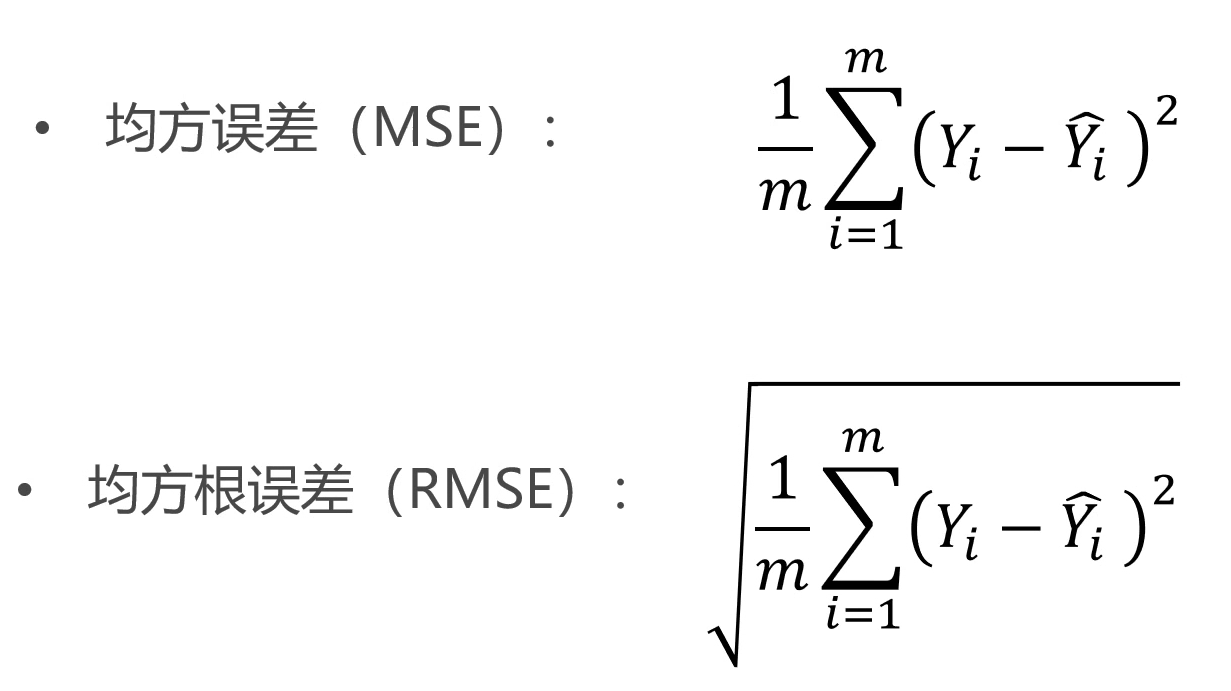
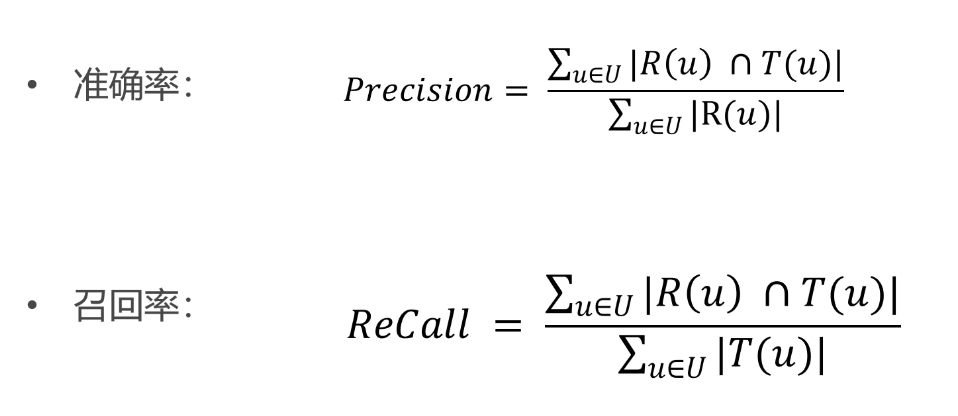
评测指标

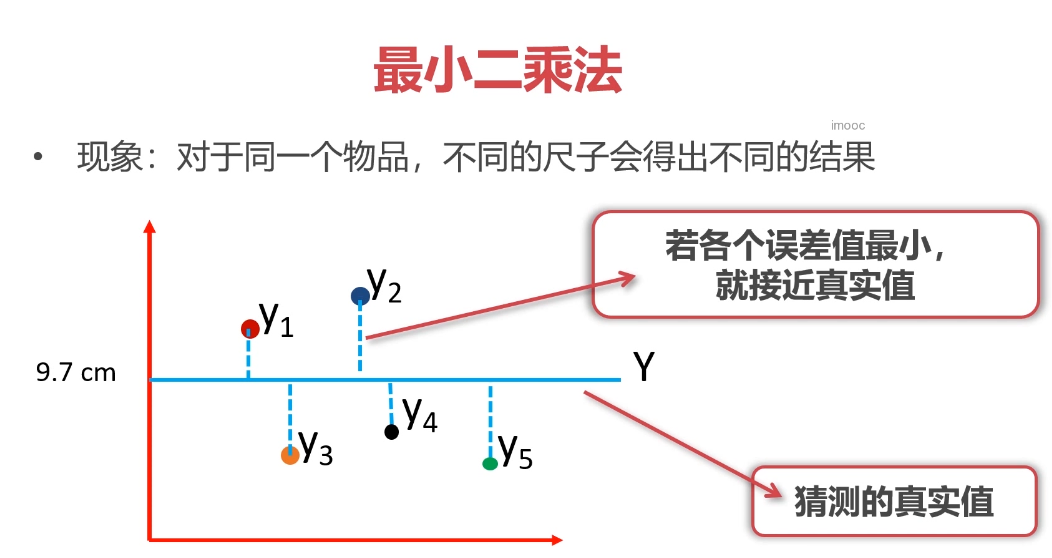
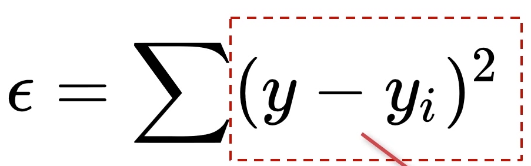
Python实现最小二乘法

import numpy as np
import matplotlib.pyplot as plt
from scipy.optimize import leastsq

data = np.loadtxt(
    "foot_high.csv",
    dtype = float,
    usecols=(0,1),
    skiprows=1,  #跳过前1行
    encoding="utf8"
)

"""
数据如下
脚长    身高
37    160
40    165
42    178
35    158
43    183
"""

x = data[:,0]
y = data[:,1]

def func(p,x):
    print("2",p)
    a,b=p
    y=a*x+b
    return y

def errors(p,x,y):
    print("p:",p)
    _y = func(p,x)
    return y-_y


res = leastsq(errors,np.array([1,1]),args=(x,y))
_a,_b=res[0]
print("a=",_a)
print("b=",_b)

print(x)
print(y)
plt.scatter(x,y,color='red')
plt.plot(x,func([_a,_b],x),color="blue")
plt.show()

关于scipy下leastsq()的一个问题

leastsq是scipy库下求通过最小二乘法求函数系数的一个函数

scipy.optimize.leastsq(func,x0,args=())  #常用形式

func 是 指误差函数，如下

def errors(p,x,y):
    _y = function(p,x)
    return y-_y

而上面errors函数中的function指的是要拟合的函数曲线：

def function(p,x):
    a,b=p
    y=a*x+b
    return y

在leastsq()的使用过程中需要注意一个问题

如下函数

def function(x,p):
    a,b=p
    y=a*x+b
    return y
def errors(x,y,p):
    _y = function(x,p)
    return y-_y
leastsq(errors,[1,1],args=[x,y])

会使得errors(x=[1,1],y=leastsq中的x,p=leastsq中的y)

因此会报错 too many values to unpack (expected 2)

因此顺序问题应该注意，正确写法如下

def errors(p,x,y):
    _y = function(p,x)
    return y-_y
def function(p,x):
    a,b=p
    y=a*x+b
    return y

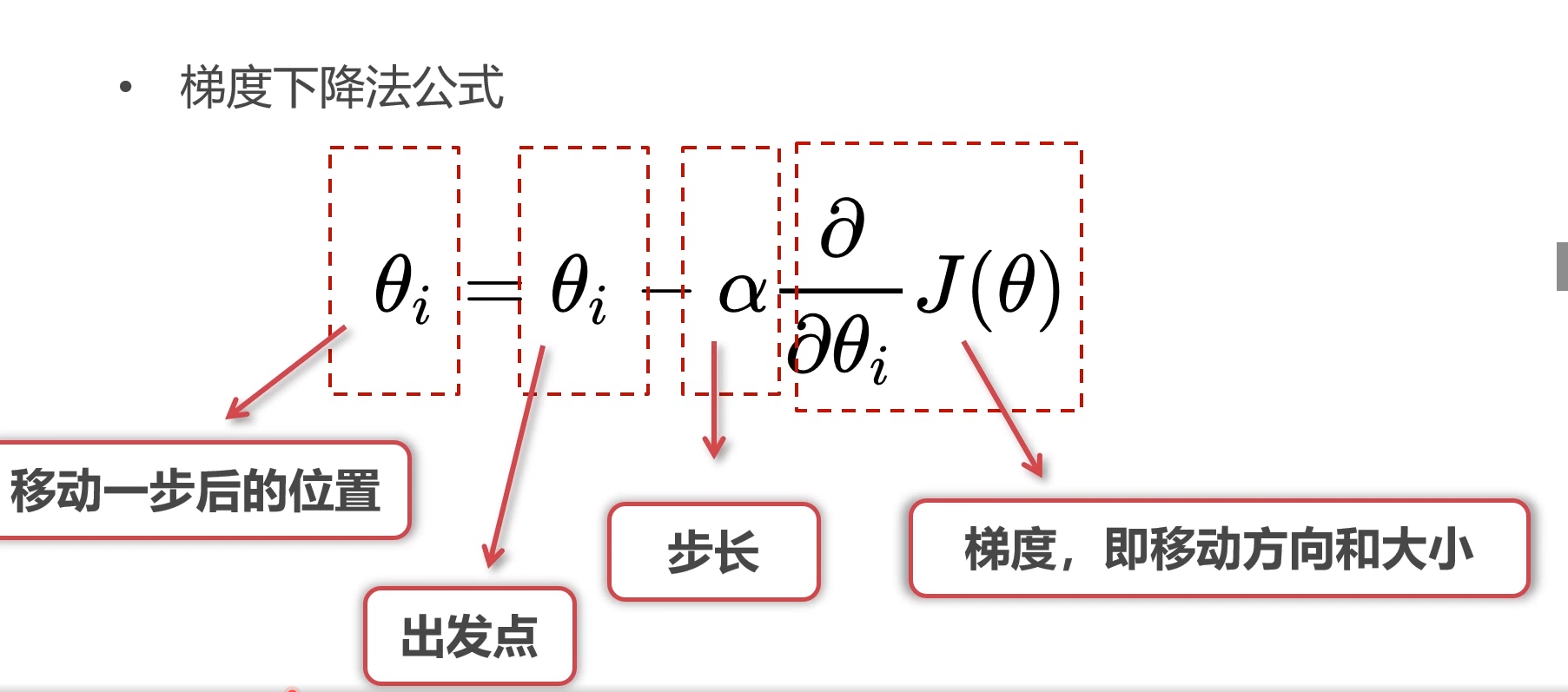
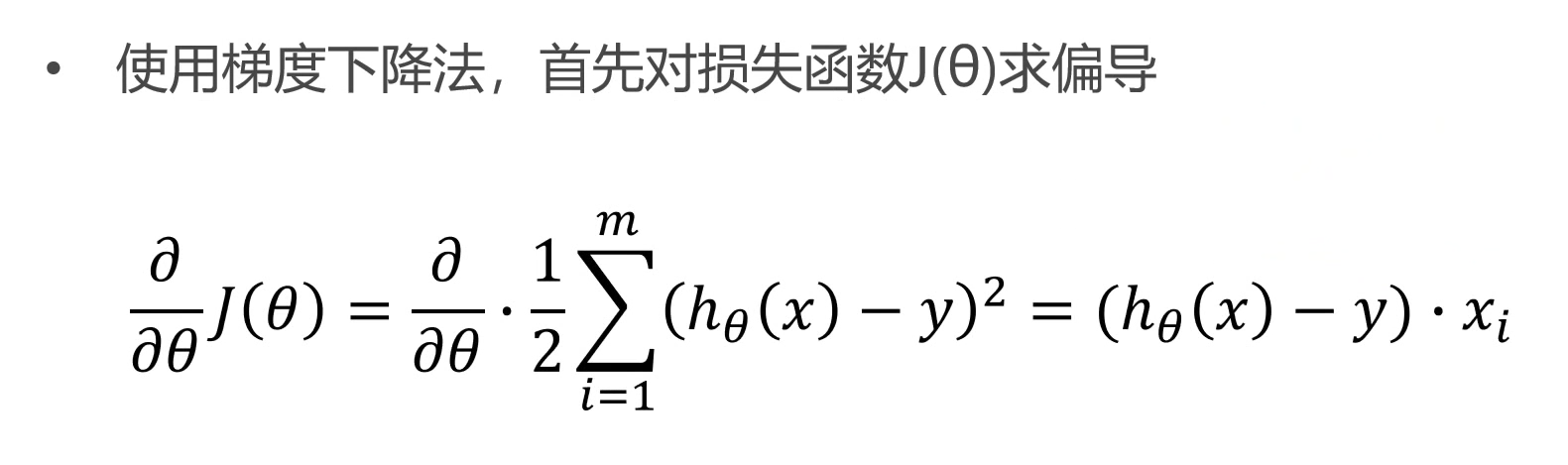
user-based